問題ページにもどる

この問題のポイント

問1　面心立方格子と体心立方格子がどんな形状になっているか、つまり、原子がどんな配置になっているのかがわかれば、この問題が解けそうです。それぞれ、こんな形状になっています。

面心立方格子	体心立方格子
それぞれの面の中心と頂点に原子がある	立方体の中心と頂点に原子がある

この問題では、面心立方格子を取り上げていますから、上の表の左側の構造となっているはずです。ということは、頂点には原子があるんですから、a，b，c，dのところには原子があります。そして、それぞれの面の中心にも原子があるんですから、辺abが通る面と辺cdが通る面の中心にも原子があります。

ただし、体心立方格子ではないので、立方体の中心に原子はありませんから、図の中央に●がある図は間違いといえます。以上のことを表している図は③となります。

ちなみに、上の図から、面心立方格子と体心立方格子それぞれに何個の原子が含まれているかもわかりますね。これも重要事項ですから、ぜひ理解しておきましょう。

面心立方格子については、8分の1の大きさとなった原子が各頂点に8個、2分の1の大きさとなった原子が各面の中心に6個ありますから、
$\displaystyle \frac{1}{8}×8+\frac{1}{2}×6$を計算して4個

体心立方格子については、まるまる1個の原子が中心に1個、8分の1の大きさとなった原子が各頂点に8個ありますから、
$\displaystyle 1+\frac{1}{8}×8$を計算して2個

問2　面心立方格子や体心立方格子について、一辺の長さと原子の半径の関係についても、参考書でよくふれられていますが、関係式をそのまま丸暗記するのではなく、計算過程をおさえて理解して覚えましょう。

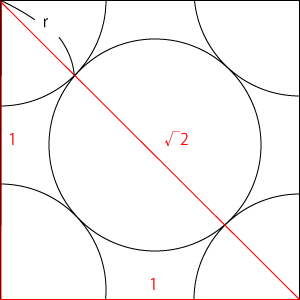
面心立方格子については、それぞれの面で原子が右の図のように配置されています。面は正方形なんですから、右の図で辺が赤色になっている三角形は直角二等辺三角形なんですから、その辺の比は$1$：$1$：$\sqrt{2}$です。

よって、単位格子一辺の長さを$a$とすると、対角線のところの長さは$\sqrt{2}a$といえます。そして、この長さは、右の図を見てわかるとおり、原子の半径$r$の4つ分と同じ長さといえますね。

なので、$\sqrt{2}a = 4r$…[1]
$\displaystyle a = \frac{4}{\sqrt{2}}r$

有理化すると、$a = 2\sqrt{2}r$です。これより、正解は②です。ちなみに、$r$について解いた式も覚えておくといいかもしれません。[1]の式を$r$について解くとこのようになります。

$\displaystyle r = \frac{\sqrt{2}}{4}a$…[2]

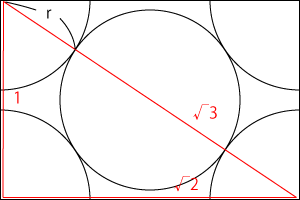
問題に出てはいませんが、体心立方格子についても同じようにしておさえておきましょう。体心立方格子については、問1の図のような切り方をした断面図で考えると、右の図のようになります。

辺が赤色になっている三角形は直角三角形ですが、今回は斜めに切っているため、一番下の辺は正方形の対角線の長さとなるので$\sqrt{2}$となっています。ということは、三平方の定理より、この直角三角形の辺の比は$1$：$\sqrt{2}$：$\sqrt{3}$です。

そして、さっきと同じように、$r$4つ分と同じ長さの辺があるので、このような式が成り立ちます。

$\sqrt{3}a = 4r$

$a$について解くと、
$\displaystyle a = \frac{4}{\sqrt{3}}r$
$\displaystyle a = \frac{4\sqrt{3}}{3}r$

$r$について解くと、$\displaystyle r = \frac{\sqrt{3}}{4}a$…[3]

問3　①：問1の解説でふれたとおり、面心立方格子には4個、体心立方格子には2個の原子が含まれているので、正しい文です。

②：問2の解説で一辺の長さ$a$について解いた式を見ると、面心立方格子と体心立方格子で違っていますので、誤りといえます。

③：1個の原子が接している数を配位数といいます。配位数は、面心立方格子については12、体心立方格子については8ですので、等しくありません。

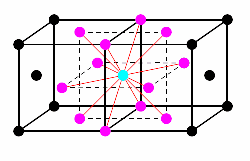
この配位数についても、丸暗記するのではなく、なぜその数になるのかを形状から把握しましょう。

面心立方格子については、それぞれの面の中心にあるのは2分の1になっている原子なので、1個の原子と考えるために単位格子を2つつなげる必要があります。そうすると、右の図のピンク色で示されている12個が隣り合っていることになるので、配位数は12となるわけです。

体心立方格子については、単位格子の中心に1個の原子がそのままありますから、それと隣り合っている個数を調べればよいだけとなります。問1の解説にある図を見て数えると、配位数は8とわかります。

④：単位格子の体積のうち原子が占める体積の割合を充填率といいます。充填率は、面心立方格子が74％、体心立方格子が68％なので、面心立方格子のほうが密だということになります。

これも丸暗記せずに、なぜそのような数値になるかを理解しながら覚えましょう。一辺の長さは$a$なのですから、単位格子の体積は$a^3$です。また、原子は球ですから、体積を考えるときは球の体積の公式を使います。その公式は下のとおりでしたね。
$\displaystyle V = \frac{4}{3}πr^3$

面心立方格子については、単位格子の中に4個の原子があり、さらに問2の解説に出てきた[2]の式を利用すると、4個の原子が占める体積は、
$\displaystyle \frac{4}{3}π×\left(\frac{\sqrt{2}}{4}a\right)^3×4 = \frac{\sqrt{2}}{6}πa^3$

$a^3$のうち、この値がどれほどの割合を占めるかというと、
$\displaystyle \frac{\sqrt{2}}{6}πa^3÷a^3 = \frac{\sqrt{2}}{6}π ≒ 0.74$

体心立方格子についても同様に考えます。これについては、単位格子の中に2個の原子があり、そして問2の解説に出てきた[3]の式を利用すると、2個の原子が占める体積は、
$\displaystyle \frac{4}{3}π×\left(\frac{\sqrt{3}}{4}a\right)^3×2 = \frac{\sqrt{3}}{8}πa^3$

さっきと同じように、$a^3$で割ると、
$\displaystyle \frac{\sqrt{3}}{8}πa^3÷a^3 = \frac{\sqrt{3}}{8}π ≒ 0.68$

⑤：面心立方格子については中心に隙間があります。

なお、結晶格子には、ほかに六方最密構造というものがあります。単位格子の中の原子数は2、配位数は12、充填率は74％となっています。

答え．
問1　③　　　問2　②　　　問3　①