この問題のポイント
円の中心が通る部分は直線と円周1つ分に分けて考える!
円が通る部分の面積は長方形3つとおうぎ形3つ(=円1個)の合計で求まる!
(1)$△ABC$の一周の長さは$4π+3π+5π = 12π$です。
そして、円$O$は半径が1なので、円周の長さは$2×1×π = 2π$です。
ということは、円$O$は$△ABC$を一周するのに$12π÷2π$ = 6回転することになります。よって、点$P$が$△ABC$の辺と接する回数も6回です。
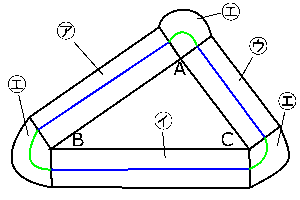
(2)円$O$の中心が動いた経路は、右の図の青色や緑色の色がついた線になります。円$O$は転がりながら移動するので、三角形の角のところを移動するときは、円の中心が動く経路は弧を描きます。青色の直線部分と緑色の曲線部分(弧の部分)をいっきに計算することはムリなので、この2つを分けて計算していきましょう。
青色の部分の長さはちょうど三角形のそれぞれの辺の長さと等しいですから、合計で$4π+3π+5π = 12π$の長さになります。
一方、3か所ある緑色の部分についてですが、この3つをつなげると1つの円になります。円$O$の半径は1ですから、3つをつなげてできた円の半径も1です。よって、緑色の部分の長さは合計で$2×1×π = 2π$です。
よって、求める長さは$12π+2π = 14π$です。
(3)円$O$が通過した部分は、さっきの(2)の図で示されています($△ABC$を取り囲んでいる図形の部分です)。この通過した部分として示されている図形の面積をいっきに計算することはできませんから、図形を分解してそれぞれの面積を考えていきましょう。
㋐~㋒の3つの部分はそれぞれ長方形です。
注意したいのは長方形の縦の長さです。さっきの(2)では円の中心が動いた経路でしたが、ここでは円$O$全体が移動した部分を考えるので、長方形の縦の長さは円$O$の直径に等しい、つまり2ですね?
なので、それぞれの長方形について、
㋐の面積…$2×4π = 8π$
㋑の面積…$2×5π = 10π$
㋒の面積…$2×3π = 6π$
そして、㋓の3つのおうぎ形についてですが、これについても3つをつなげると1つの円になります。もともとは円$O$全体が移動した部分の一部ですので、さっきの長方形の縦の長さと同様、3つをつなげてできる円の半径は2といえます。
よって、㋓の3つをあわせた面積は$2×2×π = 4π$
よって、㋐~㋓全部をたした面積は
$8π+10π+6π+4π = 28π$
(参考)
この問題のように、平面図形の外側を円がまわったあとの図形の面積は、(円の中心が動いた長さ)×(円の直径)で求まります。
例:この問題では円の中心が動いた長さは(2)より$14π$,円の直径は2なので、円が通過した面積は$14π×2 = 28π$
ただし、正式に教科書などで取り上げられている公式ではないので、「計算過程も書きなさい」などのような指示がある問題でこの解き方をすると減点になる可能性があります。答えだけ書けばいい問題や、計算間違いをしていないかの確認だけに使うほうがいいでしょう。
答え.
(1)6 (2)$14π$ (3)$28π$