この問題のポイント
2種類で表された比を1つにまとめるときは、共通する部分の数の最小公倍数を考え、それぞれの比を何倍すればいいか考える!
(1)四角形$AFCD$の面積を求めるために使える公式はありませんから、この四角形を2つの三角形に分けて考えます。そこで、$△AFD$と$△DFC$に分けて考えてみましょう。
$F$は$BD$の中点なので、$△AFD$は$△ABD$の半分の面積で、$△DFC$は$△DBC$の半分の面積です。ということは、四角形$AFCD$の面積はこのように表せることとなります。
\( △AFD+△DFC \)
\( \displaystyle = \frac{1}{2}△ABD+\frac{1}{2}△DBC \)
\( \displaystyle = \frac{1}{2}(△ABD+△DBC) \)
△ABDと△DBCを足し合わせると、台形$ABCD$になりますから、$△ABD$と$△DFC$の面積の和は\( \displaystyle \frac{1}{2}×120 \) = 60
よって、四角形$AFCD$の面積は60です。
(2)問題文で与えられている情報は、まだ面積についてのことしかありませんから、面積を利用して比を求めていくしかありません。そこで、$BE$:$ED$を求めるために、$△ABC$と$△ADC$の面積の比を考えてみます。底辺が等しい三角形の面積の比は高さの比に等しく、それと$BE$:$ED$の比は等しいからです。
さっきの(1)で四角形$AFCD$の面積を求めましたが、ここから$△AFC$をひけば$△ADC$になります。よって、$△ADC$の面積は、
60-24 = 36
すると、$△ABC$は台形$ABCD$から$△ADC$をひいた図形なんですから、$△ABC$の面積は、
120-36 = 84
これより、$△ABC$:$△ADC$ = 84:36 = 7:3
よって、$BE$:$ED$ = 7:3
(3)$F$,$G$はそれぞれ$BD$,$AC$の中点なので、$FG$//$BC$です。ということは、$△EFG$と$△EBC$は相似ですから、$FG$:$BC$ = $EF$:$EB$です。ちょうど(2)で$BD$についての比を求めたわけなので、これが使えそうですね?
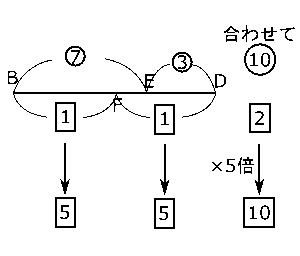
さっきの(2)で求めたとおり、$BE$:$ED$ = 7:3です。そして、$F$は$BD$の中点なので$BF$:$FD$ = 1:1です。2種類の比が使われていますが、右の図で示したとおり、$BD$が、10と2という2通りの長さで表されていることになります。同じものが2通りで表されていると考えにくいですから、これを1通りに統一するために、最小公倍数でそろえます。
10と2の最小公倍数は10ですから、$BF$:$FD$のほうを5倍すると、$BF$:$FD$ = 5:5とすることができます。すると、
$FE = BE-BF$
= 7-5
= 2とおけます。
よって、$BF$:$FE$:$ED$ = 5:2:3とわかります。
ちなみに、$BF$:$FE$:$ED$のような3項以上の比を連比といいます。
これより、$EF$:$EB$ = $EF$:$EF+BF$ = 2:7なので、$FG$:$BC$ = 2:7です。
(4)四角形$EFHG$の面積は公式を使って求めることはできないような感じがしますから、さっきの(1)と同じように2つの三角形に分けて求めていくことを考えましょう。まずは、$△EFG$の面積を考えます。
$G$は$AC$の中点で$△AFC$の面積が24なので、$△AFG$の面積は12です。その$△AFG$の中にある$△EFG$と$△AEF$ですが、$GE$と$AE$を底辺とみなせば、高さが同じ三角形の面積の比は底辺の比に等しいので$GE$:$AE$を考えると$△EFG$の面積が求まりそうですね?
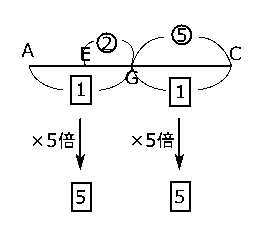
さっきの(3)で考えたとおり、$△EFG$と$△EBC$は相似で、$EG$:$EC$ = 2:7なので、$EG$:$GC$ = 2:5です。そして、$G$は$AC$の中点だから$AG$:$GC$ = 1:1です。
$GC$が5と1という2通りの長さで表されているので、最小公倍数の5にそろえるために$AG$:$GC$を5倍すると、$AG$:$GC$ = 5:5となります。すると、
$AE = AG-EG$
= 5-2 = 3とおけます。
なので、$AE$:$EG$:$GC$ = 3:2:5ですから、$AE$:$EG$ = 3:2なので、$△EFG$の面積は
\( \displaystyle \frac{2}{3+2}×△AFG \)
\( \displaystyle = \frac{2}{5}×12 = \frac{24}{5} \)
次に、$△FGH$の面積を考えます。$△AFG$と同様に、$△FGC$の面積も12です。その$△FGC$の中にある$△FGH$と$△GHC$の面積の比は$FH$:$HC$に等しいです。ここで、$FG$//$BC$なので、$△FGH$と$△CBH$は相似ですから、
$FH$:$CH$ = $FG$:$CB$ = 2:7
なので、$△FGH$の面積は
\( \displaystyle \frac{2}{2+7}×△FGC \)
\( \displaystyle = \frac{2}{9}×12 = \frac{24}{9} \)
よって、四角形$EFHG$の面積は、
\( △EFG+△FGH \)
\( \displaystyle = \frac{24}{5}+\frac{24}{9} \)
\( \displaystyle = \frac{216}{45}+\frac{120}{45} \)
\( \displaystyle = \frac{336}{45} = \frac{112}{15} \)
(別解)
$△EFG$の面積を考えるときに、$AE$:$EG$:$GC$の連比を求めましたが、連比を使わなくても考えることができます。
$FG$と$AD$は平行なので、$△ADE$と$△GFE$は相似で、その相似比は$DE$:$FE$に等しいです。
さっきの(3)で$BF$:$FE$:$ED$ = 5:2:3と求めましたので、$DE$:$FE$ = 3:2です。
よって、$AE$:$GE$ = $DE$:$FE$ = 3:2より、$△EFG$の面積は
\( \displaystyle \frac{2}{3+2}×△AFG \)
\( \displaystyle = \frac{2}{5}×12 = \frac{24}{5} \)
答え.
(1)60 (2)7:3
(3)2:7 (4)\( \displaystyle \frac{112}{15} \)