この問題のポイント
三角形の三辺から、三平方の定理を使って三角形の高さを求めるやり方をおさえよう!
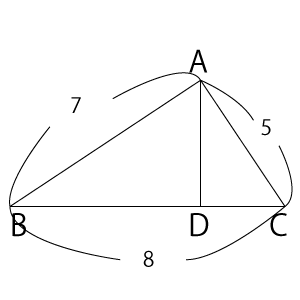
(1)問題文に書かれていたことを図にすると、右図のようになります。
ここで、$BD$を求めないといけないのですから、$BD$の長さを$x$とおきましょう。そうすると、右図からわかるとおり、とりあえず、$CD$の長さは$8-x$だとなります。
そして、ここで、$AD$は垂線だということに着目しましょう。垂直になっているわけですから、△$ABD$と△$ACD$は直角三角形だということになります。そうすると、この2つの三角形で、三平方の定理が成り立つことになりますね。
たとえば、△$ABD$についてだったら、
\( AB^2 = BD^2+AD^2 \)
が成り立ちます。ただ、残念ながら、$AD$の長さがわかりませんので、これはとりあえず、$y$とおくことにすると、
\( 7^2 = x^2+y^2 \)…①
一方、△$ACD$についてだと、
\( AC^2 = CD^2+AD^2 \)
で、$AD$はとりあえず$y$としているので、
\( 5^2 = (8-x)^2+y^2 \)…②
さて、このように2つの式ができ、連立方程式になりました。つまり、これを解けば、$x$も$y$も求まるというわけですね。ここで、よくよく見ると、2つの式にはどちらも「$y^2$」が含まれています。これを消すと、うまく解けそうですよね。
つまり、まず①の式で、$x^2$を左辺に持っていき、その後左辺と右辺を入れ替えると、
\( y^2 = 7^2-x^2 \)…③
③を②に代入すると、
\( 5^2 = (8-x)^2+7^2-x^2 \)
これで、$y^2$は消えました。あとは、これを計算して解きましょう。
\( 25 = 64-16x+x^2+49-x^2 \)
\( 25 = -16x+113 \)
\( 16x = 88 \)
\( \displaystyle x = \frac{11}{2} \)
$x$はもともとは$BD$の長さだったんですから、これで$BD$の長さが求まりましたね。
(2)三角形の面積なんですから、底辺と高さがわからないと面積を求めることはできません。一番右上の図から考えると、ちょうど$BC$が底辺になっています。そうすると、垂線が引いてあるのですから、$AD$が高さとなりますね。
$BC$の長さはすでにわかっていますから、あとは$AD$の長ささえわかれば面積が求まります。そして、$AD$については、すでに(1)で$y$とおいて、方程式を作っていましたよね。これを利用しましょう。
さっきの問題で、$x$について求まりましたから、これを代入すると、$y$が求まりそうです。①の式に代入しましょう。
\( \displaystyle 7^2 = (\frac{11}{2})^2+y^2 \)
\( \displaystyle 49 = \frac{121}{4}+y^2 \)
\( \displaystyle y^2 = \frac{75}{4} \)
$y$は$AD$の長さをあらわしているんですから、正の数に決まっています。よって、
\( \displaystyle y = \frac{5\sqrt{3}}{2} \)
これで$AD$の長さ、つまり高さが求まりました。三角形の面積は底辺×高さ÷2で求まるので、
\( \displaystyle 8×\frac{5\sqrt{3}}{2}÷2 = 10\sqrt{3} \)
このように、三辺の長さがわかっている三角形では、2つの直角三角形で三平方の定理を使って連立方程式をつくり、それを解いて高さを求めれば、面積が求まっていくんです。
(3)辺の長さしかわからない条件下で、「角度を求めなさい」となった場合、よく出てくるパターンが、特別な直角三角形の角度になることです。
つまり、「90°と45°と45°」、「90°と60°と30°」になるパターンです。
これについては、辺の比がカギになりますから、辺の長さをチェックしておきましょう。
せっかくですから、求めた辺の長さを使いたいところです。なので、△$ADC$で考えてみましょう。そうすると、さっきの計算で
\( \displaystyle AD = \frac{5\sqrt{3}}{2} \)
と求まっています。そして、
\( AC = 5 \)
ともわかっています。そして、$DC$についてですが、これは$BD$の長さを求めたんですから、これを使うと、
\( \displaystyle DC = 8-\frac{11}{2} = \frac{5}{2} \)
これで、三辺の長さがわかりました。ここで三辺の長さの比をとると、
\( \displaystyle DC:AC:AD = \frac{5}{2}:5:\frac{5\sqrt{3}}{2} = 1:2:\sqrt{3} \)
となります。つまり、「90°と60°と30°」のパターンの直角三角形だったというわけですね。そして、辺の比から判断して、$∠C$は60°だということになります。
答え.
(1)\( \displaystyle \frac{11}{2} \)
(2)\( 10\sqrt{3} \)
(3)60°