この問題のポイント
弧の長さを求めるには中心角が重要!中心角が何度になるか考えよう!
この問題の図形は、直径が10cmの円の一部でできたおうぎ形ですね。弧$AC$は、その円周の何分のいくつかがわかれば、長さが求まります。何分のいくつかを知るための、一番簡単なカギが中心角です。
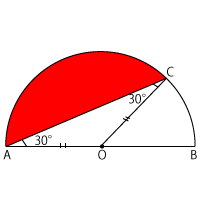
そこで、弧$AC$の中心角を知るために、右図のように$OC$に補助線をひきます。これで、$∠AOC$が中心角だとわかるので、この角度がいくつかを考えればよいということになります。
すると、$AO$も$OC$もどちらも半径なのですから、長さは等しいはず。つまり、△$AOC$は二等辺三角形だということになります。このように、同じ長さの辺がないかを考えることは、図形問題を解く上で重要になってきます。
△$AOC$は二等辺三角形ですから、$∠OAC$と$∠OCA$は等しいです。$∠OAC$ = 30°と問題文にありましたから、$∠OCA$も30°ですね。
よって、$∠AOC$は、
$∠AOC$ = 180°-$∠OAC$-$∠OCA$ = 180°-30°-30° = 120°
これで、中心角は求まりました。つまり、求める長さは、「直径が10cmの円から切り取った、120°が中心角のおうぎ形」の弧の長さということになります。なので、その長さは、
\( \displaystyle 10×π×\frac{120°}{360°} = \frac{10}{3}π \)(cm)
(別解)
弧$AB$から弧$BC$の長さをひくという求め方もあります。
弧$AB$は直径10cmの円の半円ですから、
\( 10×π÷2 = 5π \)(cm)
弧$BC$についても、さっきと同じように中心角、つまり$∠BOC$を求めないと、長さを求めることはできません。さっきのように補助線をひくと、$∠AOC$が120°と求まりますから、$∠BOC$は、
180° -120° = 60°
よって、「直径が10cmの円から切り取った、60°が中心角のおうぎ形」ですから、
\( \displaystyle 10×π×\frac{60°}{360°} = \frac{5}{3}π \)(cm)
これが弧$BC$の長さなので、弧$AC$は
\( \displaystyle 5π-\frac{5}{3}π = \frac{10}{3}π \)(cm)
答え. \( \displaystyle \frac{10}{3}π \)(cm)