この問題のポイント
ひし形は4つの辺が等しい平行四辺形
→△ABDは二等辺三角形ということに着目し、底角を求めていこう!
ひし形は4つの辺の長さが等しい平行四辺形です。辺の長さが等しいわけですから、4つの辺に、長さが等しいという印をつけておきましょう。
そして、角度を求める問題では、その角が入っている三角形に着目するのが、まず最初のやり方です。この問題の場合だと、$∠DAB$が入っている三角形なので△$ABD$になりますね。
その△$ABD$をよく見ると、2つの辺($AB$と$AD$)に長さが等しい印がついています。ということは、△$ABD$は二等辺三角形ということになりますね。
ということは、$∠ABD$か$∠ADB$のどちらかが求まってくれれば、計算して$∠DAB$の大きさが求まりそうです。
ただし、もちろん、$∠ABD$か$∠ADB$のどちらも、この図からすぐに導き出すことは難しそうです。その場合は、自分の求めたい角度と等しい角度はないかを探しましょう。
たとえば、この問題ならば、これはひし形、つまり平行四辺形なわけですから$AB$//$DC$ですね。
ということは、錯角が等しいので、$∠ABD$ = $∠BDC$です。なので、$∠BDC$を求めることを考えましょう。
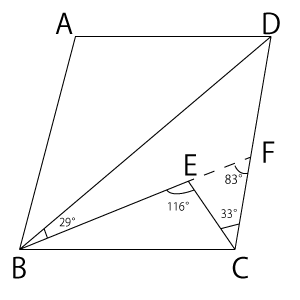
この$∠BDC$を含んでいる図形は、なんだか三角形が2つ組み合わさったような形をしていますね。そこで、補助線をひいて、三角形を2つにしてしまいましょう。右図のようにして、補助線をひきます。
そうすると、△$EFC$で、
\( ∠BEC = ∠EFC +∠FCE \)
となりますね。
(外角は、それと隣り合わない2つの内角の和に等しいからです)
ということは、116°= $∠EFC$ +33°
$∠EFC$ = 83°となります。
そして、△$DBF$において、同じように考えれば、
\( ∠EFC = ∠DBF +∠BDC \)
ですね。
よって、83°= 29°+$∠BDC$
$∠BDC$ = 54°
です。
これで、$∠BDC$が求まりました。これで、$∠ABD$の角度も$∠ADB$の角度も54°とわかりましたから、
$∠DAB$ = 180°- 54°- 54°= 72°
答え. 72°