この問題でおさえておきたいこと
一定の力を加えられている物体は速さが一定の割合で増える!
動いている物体は力を加えられていないなら等速直線運動をする!
解答
(1)
0.1秒
(2)
18cm/秒
(3)
30cm/秒
(4)
① 12 ② 等速直線
③ 約85 ④ 慣性
(5)
21.6cm
(6)
① ア ② オ ③ キ
重要事項のまとめ
・力が加わる運動
物体に力を加えると、物体の動き、つまり速さが変化する。
動いている物体に対して、動いている向きと同じ向きの力を加えれば速さは大きくなり、反対向きの力を加えれば速さは小さくなる。
物体に力を加えると、その加えた力の大きさに応じて速さが変化する。
物体に一定の力をつねに加えていると、一定の割合で物体の速さが変化する。
例:自由落下運動(物体が落下しているときの運動)
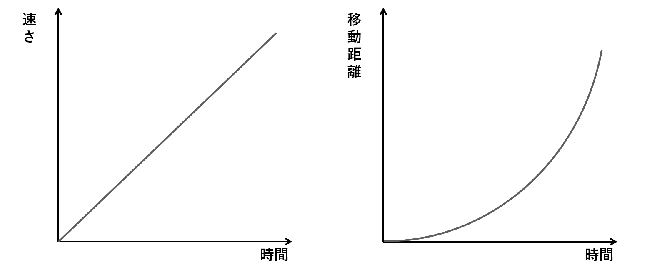
自由落下しているとき、物体には重力というつねに一定の下向きの力がかかっている。よって、自由落下しているときの物体の速さは一定の割合でどんどん速くなる。時間に比例して増えるわけなので、下の図の左にあるグラフのように、速さが変化する。
速さがどんどん大きくなっていくので、移動距離(どれだけの距離を落下するか)も、それに応じてどんどん長くなっていく。それをグラフにしたのが下の図の右にあるグラフで、時間の2乗に比例して増える(時間の2次関数で増える)。
・力が加わっていないときの運動
物体に力が加わると速さが変化する。逆にいえば、動いている物体に力がはたらかなければ速さは変化せず一定となる。このような、物体が一定の速さでまっすぐ進んでいく運動を等速直線運動という。
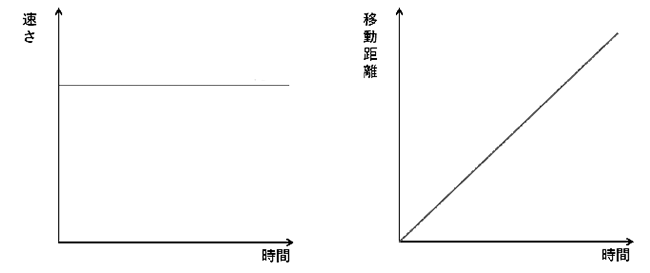
変わらず一定なので、時間と速さの関係をグラフにすると、下の図の左にあるグラフのような直線になる。
同じ速さで進んでいくので、時間と移動距離の関係をグラフにすると、時間に比例して増える形になるので、下の図の右にあるグラフのようになる。
・慣性の法則
静止している物体は静止し続けようとし、動いている物体は等速直線運動をし続けようとする。これを慣性の法則という。
解説
(1)紙テープ1本あたりには点が6個打たれています。よって、紙テープ1本のはばは6打点する間の時間を示していることになります。記録タイマーは1秒間に60打点しますから、6打点する時間は、
1÷60×6 = 0.1秒
(2)図2より、ADの長さは5.4cmです。そして、AD間の打点をした紙テープはB,C,Dの点で切られましたから3本あるはずです。(1)より、紙テープ1本がつくられるのに0.1秒かかりますから、AD間の打点をするまでに0.1×3 = 0.3秒かかります。
平均の速さは、距離÷時間で求めることができます(数学の計算と同じ)から、求める速さは、
5.4〔cm〕÷0.3〔秒〕 = 18〔cm/秒〕
(3)図2より、ACの長さは2.4cm,ADの長さは5.4cmなので、CDの長さは5.4-2.4 = 3.0cmです。CD間の打点をした紙テープは途中で切られてはいませんので1本だけしかありません。よって、CD間を移動した時間は0.1秒ということになるので、平均の速さは、
3.0〔cm〕÷0.1〔秒〕 = 30〔cm/秒〕
(4)① (3)と同じように考えると、AB間は0.6cm,BC間は1.8cm,CD間は3.0cm,DE間は4.2cm,EF間は5.4cmですから、それぞれにおける平均の速さは6cm/秒,18cm/秒,30cm/秒,42cm/秒,54cm/秒となります。これを見ると、0.1秒ごとに12cm/秒ずつ速さがふえていることがわかります。
② 糸が台車を引かなくなるということは、力学台車に力がもうはたらかないということになります。「重要事項のまとめ」にあるとおり、動いている物体はそのまま等速直線運動をしようとします。
③ 等速直線運動をしているときは速さは変わりませんから、0.1秒という決まった時間で動く距離も一定になります。図3で紙テープの長さが変化していないところがありますが、まさにこのときに等速直線運動をしているということになります。
その長さを読み取ると、約8.5cmであり、これが0.1秒で移動した距離ということになるので、そのときの力学台車の速さは、
8.5〔cm〕÷0.1〔秒〕 = 85〔cm/秒〕
④ 「重要事項のまとめ」を参照してください。
(5)図3にて、6本目の紙テープより7本目の紙テープのほうが長いことから、0.6秒後ではまだおもりが床についていないとわかります。なので、0.6秒後の打点をGとすると、AB,BC,CD,DE,EFと1.2cmずつ長くなっていたことから、FG間は5.4+1.2 = 6.6cmと考えることができます。
図2より、AF間の長さは15.0cmなので、AG間の長さは15.0+6.6 = 21.6cmです。これが0.6秒間に力学台車が移動した距離ですね。
(6)① 力学台車にはたらく力が大きくなるので、力学台車の速さのふえ方も大きくなります。
② ただの自由落下でしたら、物質の重さに関係なく同じ割合で速さがふえていきます。しかし、この問題では力学台車を引いているため、おもりの重さが重くなればなるほど速さの増加する割合は大きくなります。なので、床に達するまでの時間は短くなります。
③ 力学台車の速さが増加する割合が大きくなり、それにより、おもりが床に達したときの力学台車の速さは速くなります。その後はその速さで等速直線運動をすることになるので、おもりが床に達したあとの力学台車の速さは、質量を大きいものに変える前より速くなっています。