この問題でおさえておきたいこと
定滑車ではひもを引く力も引く長さも変わらないが、動滑車ではひもを引く力は半分になり、引く長さは2倍になる!
解答
(1)
( X )…\( \displaystyle \frac{1}{2} \) ( Y )…2
(2)
6cm
(3)
(4)
2.04J
重要事項のまとめ
・滑車の種類
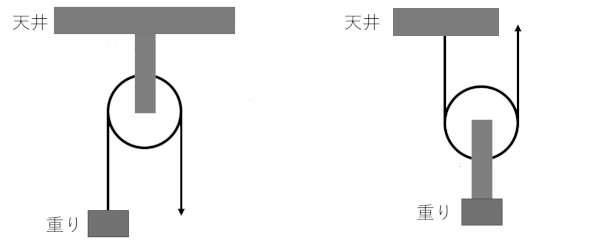
- 定滑車…
図の左側のような、軸が天井などに固定されて動かない滑車
これを使うと、力の向きを持ち上げる方向と逆向きに変えることができる - 動滑車…
図の右側のような、軸が天井などに固定されていない滑車で、ひもを引くと滑車が重りといっしょに持ち上がる
天井からのひもともう一方のひもの2本で支えられている形になっている
・滑車を使った仕事
定滑車を使った場合、ひもを引く向きを変えただけなので、必要な力もひもを引く長さも変わらない
動滑車を使った場合、2本のひもで支えられた形になっているので、手で引く力は物体の重さの半分になる
ただし、動滑車の左右両方のひもを引くことになるので、人がひもを引く長さは2倍になる
・仕事の原理
仕事は力の大きさ×その力の向きに動いた距離で求まるが、ふつうに持ち上げた場合と定滑車を使った場合では、必要な力もひもを引く長さも変わらないので、仕事の量は変わらない
一方、動滑車を使った場合でも、必要な力は半分になるが、ひもを引く長さは2倍になるので、仕事の量は結局変わらない
このように、道具を使っても使わなくても仕事の量は変わらないことを仕事の原理という
解説
(1)「重要事項のまとめ」を参照してください。
(2)図の状態(まだ糸2を引いてすらいない状態)では、糸1の分の高さは7-5 = 2cmあります。そして、動滑車を5cm引き上げたわけですから、結局動滑車を引き上げた後では、糸1の分の高さは2+5 = 7cmあることになります。
この状態から糸1がまっすぐな状態になるまで引き上げるわけです。糸1の長さは10cmですから、動滑車をあと10-7 = 3cm引き上げる必要がありますね?
ただし、「重要事項のまとめ」にあるとおり、動滑車を引き上げるときは糸を引く長さは2倍になるのですから、引かなければならない糸2の長さは3×2 = 6cmです。
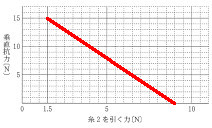
(3)垂直抗力とは、床が物体を支える上向きの力のことで、床が受けている重力に押し返す形で発生する力です。この実験の図を見ると、床は動滑車とおもりの2つの物質の重力を受けていますから、その分を押し返す形で垂直抗力が生じます。
しかし、おもりは糸2で引かれており、糸2は上向きの力で引っ張られているのですから、その力が大きければ大きいほど、垂直抗力は少なくすみます。そして、糸2は動滑車につながっているわけなので、おもりにとっては糸2を引く力の2倍の力で上に引っ張られるはずですね?
よって、おもりが床から受ける垂直抗力は、
(動滑車の重力)+(おもりの重力)-(糸2を引く力)×2
と計算することができるわけです。
動滑車の質量は300g(=3N)でおもりの質量は1500g(=15N)なので、重力としては3+15 = 18Nかかるので、結局、18-(糸2を引く力)×2という関係になります。
これより、糸2を引く力が1.5Nのときは垂直抗力は15Nとわかり、糸2を引く力が9Nのときに垂直抗力が0となっておもりが床から離れるとわかります。
(4)仕事は力の大きさ(N)×その力の向きに動いた距離(m)で求めることができます。その公式を使って考えていきましょう。
まず、糸1がまっすぐな状態になるまでに引いたときの仕事を考えます。(2)で考えたとおり、図の状態(まだ糸2を引いてすらいない状態)では、糸1の分の高さは7-5 = 2cmあるので、糸1をまっすぐにするためには、10-2 = 8cm(=0.08m)引く必要があります。
そのときの力の大きさは、ばねばかりの値で1.5Nですが、(3)で考えたとおり、おもりや糸にとってはその値の2倍の力で上に引っ張られるわけなので、糸1がまっすぐな状態になるまでに引いたときの仕事は、
1.5×2×0.08 = 0.24J
次に、おもりが床から離れて10cm引き上げられたときの仕事を考えます。引き上げられた高さは10cm(=0.1m)ですが、そのときの力の大きさは(3)のグラフより9Nですね?さっきと同じように考えると、
9×2×0.1 = 1.8J
よって、求める仕事は、
0.24+1.8 = 2.04J