この問題でおさえておきたいこと
直列回路は電流がどこも同じで電圧・抵抗はそれぞれのものをたした値が全体のものになる!
並列回路は電圧がどこも同じで電流はそれぞれのものをたした値が全体のものになる!
解答
(1)5A
(2)2A
(3)30V
(4)5A
重要事項のまとめ
・直列回路や並列回路全体の電流・電圧・抵抗
1.直列回路
電流…それぞれの抵抗を流れる電流はどこも等しい(回路全体の電流もそれぞれの抵抗を流れる電流と等しい)
電圧…それぞれの抵抗での電圧の和に等しい(それぞれの抵抗での電圧をたせばいい)
抵抗…それぞれの抵抗の値の和に等しい(それぞれの抵抗の値をたせばいい)
2.並列回路
電流…それぞれの抵抗を流れる電流の和に等しい(それぞれの抵抗を流れる電流をたせばいい)
電圧…それぞれの抵抗での電圧はどこも等しい(回路全体の電圧もそれぞれの抵抗での電圧と等しい)
抵抗…回路全体の抵抗を$R$、それぞれの抵抗を$R_1$,$R_2$,…とすると\( \displaystyle \frac{1}{R} = \frac{1}{R_1}+\frac{1}{R_2}+… \)が成り立つ
解説
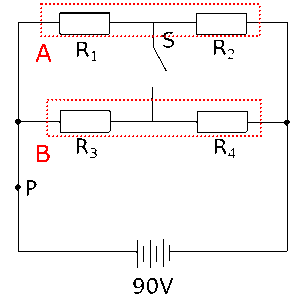
(1)回路全体の電流を求めればPを流れる電流が求まります。回路全体の電圧は90Vなので、あとは回路全体の抵抗がわかれば、オームの法則を使って求めることができますね?
回路は、右の図のようにAの部分とBの部分が並列になっていると考えればいいわけですが、Aの部分とBの部分それぞれは2つの抵抗が直列につながっています。直列と並列が混ざった形になっているわけです。このような混ざった形の回路では、小さい単位の部分から抵抗や電流を計算していくことが重要です。
たとえば、この問題の場合では、Aの部分、Bの部分それぞれで抵抗はいくらになっているかということから計算していく必要があります。Aの部分、Bの部分それぞれは直列の形になっているので、
Aの部分…15+30 = 45Ω
Bの部分…10+20 = 30Ω
そして、Aの部分とBの部分は並列につながっているので、回路全体の抵抗を$R_x$とすると
\( \displaystyle \frac{1}{R_x} = \frac{1}{45}+\frac{1}{30} \)
\( \displaystyle \frac{1}{R_x} = \frac{2}{90}+\frac{3}{90} \)
\( \displaystyle \frac{1}{R_x} = \frac{5}{90} = \frac{1}{18} \)
なので、$R_x$ = 18Ω
よって、オームの法則より、回路全体の電流、つまりPを流れる電流は
90÷18 = 5A
(2)Aの部分とBの部分が並列になっているわけですから、Aの部分とBの部分それぞれの部分での電圧は電源と同じ90Vです。
そして、(1)の解説にあるとおり、Aの部分の抵抗は45Ωなので、Aの部分を流れる電流は、
90÷45 = 2A
そして、Aの部分の中身は2つの抵抗の直列になっているわけですが、「重要事項のまとめ」にあるとおり、直列回路では電流はどこも同じ数値になるわけですから、$R_1$を流れる電流も2Aということになります。
(別解)
先に(2)を解いてから(1)を解くという方法もあります。さっきの解説にあるとおりにAの部分を流れる電流を求めます(これで$R_1$を流れる電流も同時に求まります)。
そして、これと同じ方法でBの部分を流れる電流を求めます。(1)の解説にあるとおり、Bの部分の抵抗は10+20 = 30Ωなので、Bの部分を流れる電流は
90÷30 = 3A
Aの部分とBの部分は並列になっていて、「重要事項のまとめ」にあるとおり、並列回路では、回路全体の電流はそれぞれの部分を流れる電流をたせばいいわけなので、Pを流れる電流は
2+3 = 5A
(3)さっきの(別解)のところで述べたとおり、Bの部分を流れる電流は3Aです。直列になっているところは電流はどこも同じなので、$R_3$を流れる電流も3Aです。
そして、問題文で$R_3$の抵抗は10Ωとあるので、オームの法則より、$R_3$の両端の電圧は
3×10 = 30V
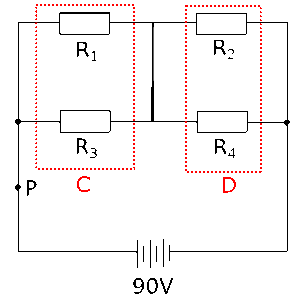
(4)スイッチSを閉じると、右の図のようになり、Cの部分とDの部分が直列になった回路になります。Cの部分とDの部分それぞれは2つの抵抗が並列につながった形になっていますね。それを念頭に、(1)と同じように回路全体の電流を求めていきましょう。
Cの部分の抵抗を$R_y$とすると、
\( \displaystyle \frac{1}{R_y} = \frac{1}{15}+\frac{1}{10} \)
\( \displaystyle \frac{1}{R_y} = \frac{2}{30}+\frac{3}{30} \)
\( \displaystyle \frac{1}{R_y} = \frac{5}{30} = \frac{1}{6} \)
なので、$R_y$ = 6Ω
Dの部分の抵抗を$R_z$とすると、
\( \displaystyle \frac{1}{R_z} = \frac{1}{30}+\frac{1}{20} \)
\( \displaystyle \frac{1}{R_z} = \frac{2}{60}+\frac{3}{60} \)
\( \displaystyle \frac{1}{R_z} = \frac{5}{60} = \frac{1}{12} \)
なので、$R_z$ = 12Ω
このCの部分とDの部分が直列につながっているので、回路全体の抵抗は
6+12 = 18Ω
よって、オームの法則より、回路全体の電流、つまりPを流れる電流は
90÷18 = 5A